主成分分析をしてみよう！

コマンドは赤字のところを入力してください！

主成分分析とは

多次元データのもつ情報をできるだけ反映して，次元を減らして，情報を縮約する方法

多次元データを２次元や３次元に縮約することで，データ全体を視覚化することができるので，データが持つ情報を解釈しやすくなる。

主成分分析の押さえるところ

• 主成分の分散→分散共分散行列（相関行列）の固有値
• 主成分分析は，分散共分散行列から分析を行う場合と，相関行列から行う場合で結果が異なる
• 尺度（単位）が異なるデータの場合，変数を基準化して分析を行う必要がある。

主成分得点を求めてみよう

下準備

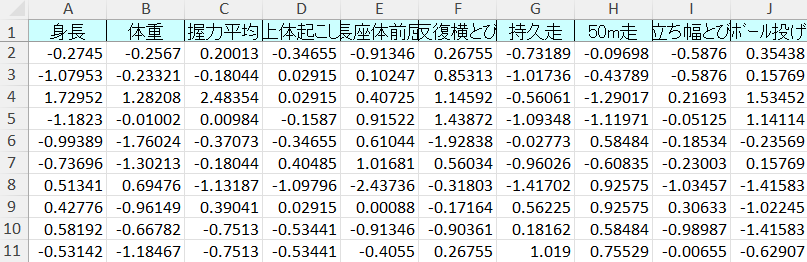
例として，下記のような標準化したデータを用意します。

手順１　ライブラリのインストール

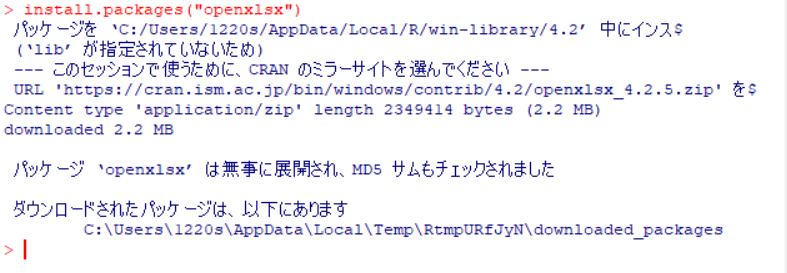
エクセルデータを読み込むために，「openxlsx」をインストールします。

install.packages("openxlsx")

手順２　エクセルを読み込む

library(openxlsx)

データフレーム名 <- read.xlsx("エクセルファイル名")

「ｄｆ」というデータフレームに格納されました。

次に，「ｄｆ」の特徴量を確認しておきましょう。

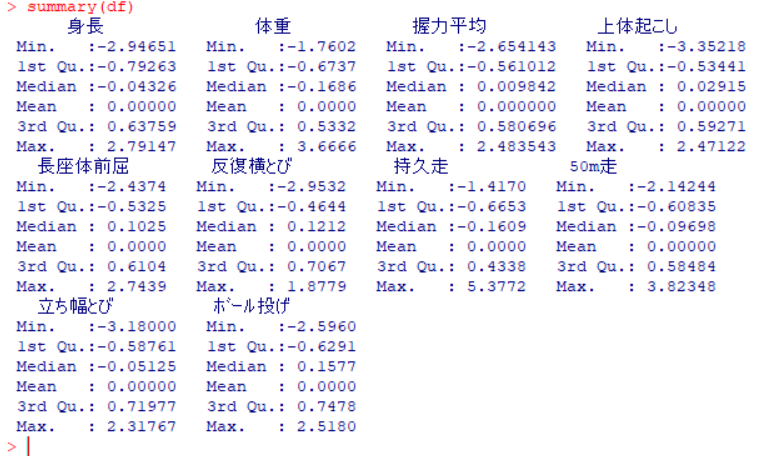
手順３　主成分分析を行う

主成分分析を行う関数【prcomp】を適用する。「ｄｆ」の主成分分析の結果を「ｄｆ１」に格納しました。

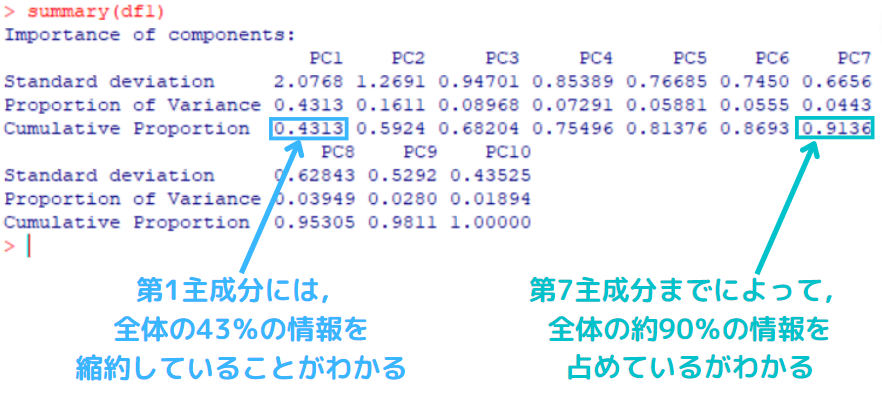
累積寄与率を読み取る。

関数【summary】を適用し，主成分分析の結果の要約を出力する。

• Standard deviation（標準偏差）
• Proportion of Variance（寄与率）
• Cumulative Proportion（累積寄与率）

手順４　分析結果の出力

①　固有ベクトルの出力

データフレーム名$rotation：固有ベクトル（主成分軸の係数）

持久走・50m走は，数値が小さい方がよいので，マイナスになっていることを考慮する。

第１主成分は「体力測定の種目の総合得点の因子」であると考えられる。

つまり，第1主成分が大きい⇒体力測定の総合得点が高い！

第２主成分は「身体測定の因子」であると考えられる。

つまり，第２主成分が小さい⇒身体測定の数値が大きい！

②　因子負荷量

１行目：因子負荷量の計算

固有ベクトル（df1$rotation）と，対応した固有値の平方根（df1$sdev）との積をとる

３行目：視覚化する（１次元）

読み取り

主成分と強い相関（0.8付近）と，主成分と弱い相関に分かれていることが視覚的にわかる。

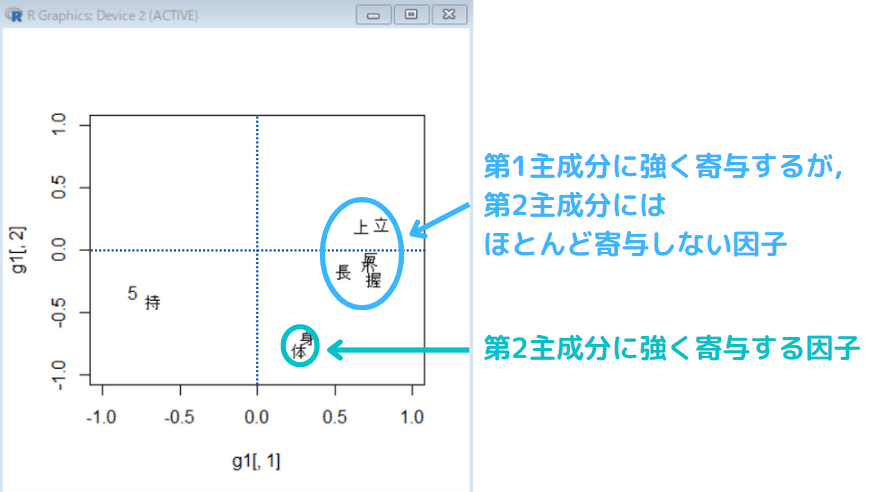
視覚化する（２次元）

第1主成分と第2主成分でプロットする。

読み取り

③　主成分得点

下記に，個々のデータを代入したもの

データフレーム名$x：主成分得点

biplot（データフレーム名）

主成分得点をプロットすると，個体の特徴や位置を把握しやすくなる。

biplot関数を適用することで，解釈しやすい形で主成分得点のプロットを得ることができる。

ちょっと詳しく

引数【scale】について，「scale=T」と「scale=F」がある。

　

• 「scale=T」→相関行列から主成分分析を行う
• 「scale=F」→分散共分散行列から主成分分析を行う

参考：統計科学研究所

https://statistics.co.jp/reference/software_R/statR_9_principal.pdf